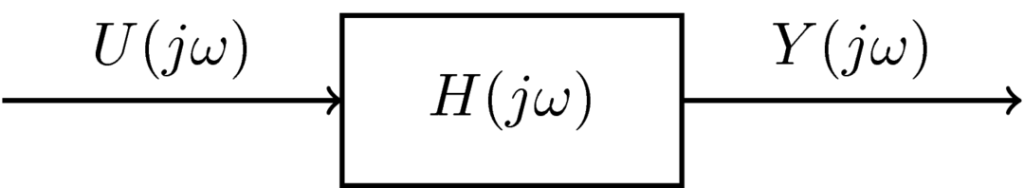Az előző néhány cikkben kifejtettem a kulcsfontosságú algoritmusokat. Most egy kicsit gyakorlatiasabb rész fog következni.

A legelső fejezetben is szó volt már arról, hogy a mintavételezett jel spektruma periodikus lesz és csak akkor reprodukálható a jel a mintáiból, ha a sávszélességél legalább kétszeres frekvenciával mintavételezzük. A probléma ott keletkezik, hogy nem mondhatjuk:

Jó lesz az! Majd biztos csak 20 kHz-ig tart majd a spektrum…

A spektrum ugyanis nem üres. Ha mással nem, zajjal terhelt, ami ugyanúgy bele tud köpni a levesünkbe, hiszen a mintavételező áramkörünk nem tudja kiválogatni a hasznos jelet. Meg kell oldani tehát, hogy a kívánt sávszélesség felett már elhanyagolható nagyságú jelek legyenek, amelyek nem zavarnak bele a hasznos jel spektrumába.

A probléma megoldására terveznünk kell egy szűrőt, ami eltávolítja a nemkívánatos spektrumkomponenseket.

Másodfokú lengőtag

Ha szeretnénk tudni, hogy a frekvencia függvényében egy valamilyen rendszer hogyan viselkedik, akkor erre az átviteli karakterisztika ad választ. Egy alapvető átviteli karakterisztika az úgynevezett másodfokú lengőtag átviteli karakterisztikája.

\begin{align}
H\left(j\omega\right)&=\frac{1}{\left(j\frac{\omega}{\omega_{0}}\right)^{2}+2\zeta j\frac{\omega}{\omega_{0}}+1}
\end{align}

Ha ábrázoljuk az úgynevezett Bode-diagramon, akkor látható hogy az \(\omega_{0}\) vágási (vagy törésponti) frekvencia felett a rendszer elnyomja a spektrumkomponenseket.

Egy ilyen rendszert jellemeznek a nevezőben lévő polinom gyökei. Ezeket pólusoknak nevezzük. Ezek a pólusok felírhatók az alábbi módon.

\begin{align}
p_{1,2}&=-\omega_{0}\zeta\pm j\omega_{0}\sqrt{1-\zeta^{2}}
\end{align}

A későbbiekben a szükséges pólusokat fogjuk meghatározni (azoknak a valós és képzetes részét). Ebből kell majd a \(\zeta\) csillapítási tényezőt meghatározni.

\begin{align}
\zeta&=\frac{1}{\sqrt{1+\left(\frac{\Im{p}}{\Re{p}}\right)}}
\end{align}

A vágási frekvencia értéke a \(22 \textrm{kHz}\)-ből számítható. Egy szűrő esetén az átmeneti sáv meredekségét a pólusok száma (és elhelyezése) határozza meg. Esetünkben három póluspárt fogunk elhelyezni, ami elég meredek vágást tesz lehetővé.

 Minimalizálási feladat megoldása Csebisev-polinomokkal

Sikerült elég rémisztőre választani az alcímet. Mint már említettem a pólusok elhelyezkedésének is meghatározó a szerepe a szűrésben. A póluselrendezést Csebisev-polinomok alapján határozzuk meg és így kialakíthatunk egy inverz Csebisev szűrőt. Hogy mi a számítás menete, azt bízzuk a Matlab-ra. Ez a függvény a cheby2 függvény.

Adjuk meg a szűrő rendszámát, ami a pólusok száma (most itt hat). A zárósávi csillapítás legyen mondjuk \(40\textrm{dB}\). Ez azt jelenti, hogy minden komponens értékét ami a zárósávban van századára csökkenti. Meg kell még adni, hogy mekkora a vágási frekvencia (ez most ugye \(22 \textrm{kHz}\)). Figyeljünk oda, hogy a függvény körfrekvenciát vár (\(\omega=2\pi f\)). A függvény normálva kéri a frekvenciát, leosztva a mintavételi frekvenciával. Mi abszolút mértékben szeretnénk a meghatározni a szűrőt, ezért használjuk az ‘s’ kapcsolót.

A “p” tömbben vannak a pólusok (a “z” tömbben az úgynevezett zérusok, erre most nincs szükség) és a “k” szám, a csillapítása a szűrőnek. Számunkra most a pólusok fontosak. Minden póluspárhoz meghatározhatjuk a csillapítási tényezőt (a fent látott összefüggés alapján):

Sallen-Key topológia

Most már csak ki kell találni, hogy ez hogyan is fog kinézni a valóságban? Egy lehetséges aktív szűrős megvalósítás, az úgynevezett Sallen-Key topológia.

 

A szokásos hálózatszámítási módszerekkel, rabszolga munka árán megmutatható, hogy ennek a rendszernek az átviteli karakterisztikája:

\begin{align}
H^{\textrm{SK}}\left(j\omega\right)=\left(1+\frac{R_{2}}{R_{1}}\right)\frac{1}{\left(j\omega RC\right)^{2}+2\left(1-\frac{R_{2}}{2R_{1}}\right)j\omega RC+1}
\end{align}

Ha összevetjük a fent tárgyalt lengőtaggal:

\begin{align}
\omega_{0}&=\frac{1}{RC}\rightarrow RC=\frac{1}{2\pi f_{0}}\\
\zeta&=1-\frac{R_{2}}{2R_{1}}\rightarrow \frac{R_{2}}{R_{1}}=2\left(1-\zeta\right)
\end{align}

A hatodfokú szűrő így:

*kép*

Válasszunk ellenállásokat az egyes fokozatokhoz. Most kulcsfontosságú a csillapítási tényezőhöz választani ezeket. Segítsük a tervezést azzal, hogy a nevezőknek minden esetben \(1\textrm{k}\Omega\).

\begin{align}
R_{11}&=R_{21}=R_{31}=1\textrm{k}\Omega\\
R_{12}&=129.5\Omega\rightarrow 120\Omega\\
R_{22}&=844.4\Omega\rightarrow 820\Omega\\
R_{32}&=1627.3\Omega\rightarrow 1.8k\Omega\\
\end{align}

A becslések miatt megváltoztak az ellenállás arányok.

Az utolsó doboz egy korrekció, mert az aktív szűrő módosít a bemenet nagyságán. Vágási frekvencia alatt jó közelítéssel \(\left(1+\frac{R_{2}}{R_{1}}\right)\) az erősítés, ezt a szűrés után “vissza kell csinálni”.

\begin{align}
K = \frac{1}{\left(1+\frac{R_{12}}{R_{11}}\right)\left(1+\frac{R_{22}}{R_{21}}\right)\left(1+\frac{R_{32}}{R_{31}}\right)}
\end{align}

Ezt a korrekciót egy feszültségosztóval fogjuk elvégezni (\(R_{01}\) és \(R_{02}\) ellenállásokon).

\begin{align}
K&=\frac{R_{02}}{R_{01}+R_{02}}\\
\frac{R_{01}}{R_{02}}&=\frac{1}{K}-1
\end{align}

Ez gyönyörűen szabvány ellenállásokból felépíthető.

Még egy gyors számítás. Határozzuk meg a kondenzátor és ellenállás értékét, ami beállítja vágási frekvenciát.

Ebből egy lehetséges választás a \(C=6.8\textrm{nF}\) és az \(R=1.2\textrm{k}\Omega\). Természetesen így nem pont \(22\textrm{kHz}\)-nél fog vágni a szűrő. Lássuk, akkor hol?

A számítások szerint körülbelül \(19.5 \textrm{kHz}\)-nél lesz a tényleges törésponti frekvencia.

Szimuláció

A kapott eredményekből felállíthatunk egy szimulációt. Én ebben az esetben az LTSpice  XVII programot választottam. Ez egy ingyenes szoftver, bárki nyugodtan ismerkedhet vele, nagyon hasznos.

A szimulációban nem a tényleges műveleti erősítőket használtam, csak kiválasztottam egyet. Ezek után egy frekvenciatartománybeli vizsgálatot állítottam be, melynek az eredménye az alábbi lett:

A sok görbe (a bemenet, az egymást követő szűrőfokozatok és a kompenzálás) között jól látható, hogy a kimenet (lila) \(40\textrm{kHz}\) frekvenciánál, már  \(40\textrm{dB}\) csillapítást mutat, mint ahogyan azt meghatároztuk.